[과학과 불교]
바닷물은 짜지 않고, 푸른 하늘은 푸르지 않다
페이지 정보
양형진 / 2022 년 10 월 [통권 제114호] / / 작성일22-10-05 10:26 / 조회3,585회 / 댓글0건본문
방향을 가리키는 나침반
나침반의 N극이 가리키는 방향을 자북磁北(magnetic north)이라고 한다. 지구가 자북을 향하는 지자기장을 만들어낸다는 것은 지구 자체가 자석이라는 것이다. 지구는 우리가 주변에서 볼 수 있는 가장 거대한 자석이다. 이 거대한 자석이 북반구에서 지표면과 만나는 지점을 자기북극(magnetic north pole)이라고 한다. 자북은 자기북극으로 가는 방향이다.

지구가 큰 자석이라면 나침반은 작은 자석이다. 같은 자석이지만 자석의 역할을 하는 원인은 아주 다르다. 지구 자기장은 지구 외핵을 흐르는 유체가 만들어낸다. 자기북극의 위치는 이 유체의 흐름이 바뀌면서 지속적으로 변한다. 또한 자기장을 휘게 하는 태양풍에 의해 달라지기도 한다. 나침반이 자석의 역할을 하는 이유는 원자와 전자의 양자역학적 특성 때문이다. 이 특성으로 인해 원자핵이나 전자 등은 아주 작은 자석이 된다.
우리 주변에 널린 자석, 자기쌍극자
고전 전자기학에 의하면, 전하는 전기장을 만들고 전류는 자기장을 만든다. 전하의 움직임이 전류이므로 정지한 전하는 전기장을 만들고 움직이는 전하는 자기장을 만든다는 것이 된다. 움직임의 특별한 경우가 원운동이다. 전하가 원운동을 하면 특별한 것이 만들어진다.
원형 회로에 흐르는 전류는 막대자석과 같은 역할을 한다. 전자석이 쉽게 확인될 수 있는 좋은 예다. 지구가 거대한 자석인 것도 아마 이 때문일 것이다. 어떤 경우건, 전하가 원운동을 하면 N극과 S극이 있는 자석이 만들어진다. N과 S의 두 자극이 있으므로, 이를 자기쌍극자(magnetic dipole moment)라고 한다.
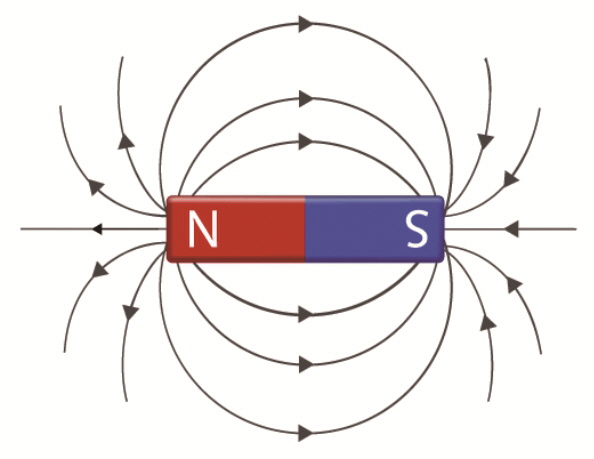
자기쌍극자는 우리 우주에 아주 흔히 존재한다. 가까이에는 나침반과 같은 영구자석, 무거운 짐을 들어올리는 전자석 등이 있다. 멀게는 수많은 항성과 행성, 위성에서 자기쌍극자가 관측됐다. 그러나 무엇보다 놀라운 일은 양자역학에서 나왔다. 양성자, 중성자, 전자 등의 기본입자가 자기쌍극자를 갖는다는 사실이 확인됐다. 이는 우리 주변의 거의 모든 것이 자석이라는 것이다.
스핀: 양자세계의 아주 작은 자석
양자역학에서는 기본입자의 자기쌍극자를 기술하기 위해 스핀spin 각운동량 혹은 줄여서 스핀이라는 물리량을 도입한다. 각운동량은 회전과 관련된다. 스핀에도 회전이란 의미가 들어 있다. 그러나 이런 정황과 달리, 스핀은 회전과 전혀 상관이 없다. 스핀이란 용어는 오히려 전하가 궤도를 따라 공전公轉(revolution)하지 않는다는 것을 강조하는 역할을 한다. 그럼 자전自轉(rotation)인가? 그것도 아니다. 크기가 점처럼 작은 전자가 아무리 빨리 자전해도, 관측되는 자기쌍극자를 만들어낼 수는 없다.
이는 중성자를 보면 더욱 명확해진다. 중성자에는 전하가 없으므로, 어떤 회전운동을 하더라도 자기쌍극자를 만들어낼 수 없다. 그럼에도 불구하고 양성자나 전자처럼, 중성자도 자기쌍극자를 갖는다. 이처럼 고전물리학의 회전운동으로는 기본입자의 자기쌍극자를 설명할 수 없다. 양성자, 중성자, 전자 같은 기본입자는 회전이나 전하와 상관없이 그 자체로 자기쌍극자가 형성돼 있다. 그 자체가 자석이다. 이렇게 회전운동 없이 자기쌍극자를 만들어내는 물리량을 스핀이라고 한다. 스핀은 철저하게 양자역학적인 개념이다.
스핀 측정: 주관이 설정한 범주 안에서 객관의 모습이 나타난다
전자의 스핀이 향하는 방향을 측정한다고 하자. 3차원 공간에는 무한히 많은 방향이 있지만, 나를 기준으로 (전후), (좌우), (상하)의 세 방향을 생각할 수 있다. 이는 3차원 공간의 세 축에 해당한다. 전자스핀의 측정값은 up/down의 두 가지만 존재한다. 왜 그런지는 모르지만, 자연이 그렇다. 점수를 공개하지 않고 합격/불합격만 발표하는 시험과 같다.
이제 스핀의 (전후) 방향을 측정한다고 하자. 측정값은 up이나 down 중 하나다. 이는 스핀이 앞이나 뒤를 향해 있다는 것이다. (전후)-측정을 했는데, 스핀이 왼쪽이나 오른쪽, 혹은 위나 아래로 향하는 결과가 나오지는 않는다. (전후)-측정을 하면 언제나 (앞)이나 (뒤)라는 측정값이 나온다. 어찌 보면 당연히 그래야 할 것 같기도 하지만, 여기엔 양자역학의 아주 중요한 기본 특성이 숨어 있다. 살펴보자.
(전후), (좌우), (상하) 중에 어떤 측정을 할지는 관측하기 전에 정해야 한다. 이는 어떤 물리량을 측정할지를 결정하는 일이고, 관측자가 판단해야 할 일이다. (전후)-측정을 하겠다고 결심하면 (앞)이나 (뒤)라는 측정값이 나타나고, (상하)-측정을 하겠다고 결심하면 (위)나 (아래)라는 측정값이 나타난다. (전후)-측정을 하겠다는 것은 관측하기 전에 관측자가 결정해야 할 일이고, (앞)이나 (뒤)라는 측정값은 관측을 통해 나타나는 결과다. 이처럼 관측 결과인 측정값은 관측을 통해 드러나지만, 측정값의 범주는 측정하기 전에 미리 정해진다.(주1)

관측자의 의도에 따라 측정값의 범주가 정해지는 것이 스핀만은 아니다. 양자역학이 다루는 물리량이 전부 그렇다.(주2) 그러므로 양자역학의 측정은 대상의 속성을 객관적으로 모두 드러내는 것이 아니다. 주관이 측정값의 범주를 설정하고, 그렇게 설정한 영역 안에서 대상의 모습이 나타난다. 하이젠베르크Heisenberg가 말한 바와 같이, 관측이라기보다는 참여라고 하는 것이 양자역학의 측정을 더 타당하게 묘사하는 것일 수 있다.
주관이 설정한 범주에 의해 대상이 달라진다
연속적인 측정에서는 더욱 놀라운 상황이 벌어진다. 처음에 (전후)-측정을 했고, 측정값이 (앞)이었다고 하자. 다시 (전후)-측정을 한다면 (앞)이라는 측정값을 반복해서 확인할 수 있다. 그러면 이 전자의 스핀은 앞으로 향한 상태에 있다고 생각하게 된다. 여기까지는 당연하다. 이와 달리, 다른 측정을 하게 되면 일상적인 관점으로는 이해하기 어려운 상황이 발생한다.
(앞) 방향은 (위/아래)가 아니고 (왼쪽/오른쪽)도 아니다. (앞) 방향이 (위/아래)가 아니므로, 고전적으로 보면 두 번째로 (상하)-측정을 했을 때 (위)나 (아래)라는 측정값이 나오면 안 된다. 그러나 두 번째로 (상하)-측정을 하면 이 측정이 설정하는 측정값의 범주인 (위/아래) 중의 하나가 관측된다. 이는 (좌우)-측정을 하더라도 마찬가지다. (왼쪽/오른쪽) 중의 하나가 관측된다. 어떻게 (앞)으로 향했던 스핀이 (위/아래)나 (왼쪽/오른쪽)으로 방향이 바뀔 수 있는가? 고전적인 관점으로는 이해하기 어렵다.
이제 세 번째로 (전후)-측정을 한 번 더 해 보자. 처음 두 번의 측정에서 (앞)과 (위)가 관측됐다고 하자. 세 번째 (전후)-측정을 하면 (앞)과 (뒤)가 관측될 확률이 50%로 같다. 이는 실험적 사실이다. 처음 측정에서 (앞)이 관측됐던 전자가 세 번째 측정에서는 (앞뒤) 어느 방향으로나 관측된다는 것이다. 양자역학의 논리로 보면 아주 간단하다. 세 번째로 (전후)-측정을 준비하면서 (앞/뒤)라는 측정값의 범주가 만들어졌기 때문이다.
이게 고전적인 관점에서는 이해되지 않는다. 처음 측정에서 (앞)이 관측됐는데 두 번째 측정에서 (위)가 관측됐다는 것도 이해하기 어렵지만, 세 번째 측정에서 (앞)과 (뒤)가 같은 확률로 관측된다는 것은 더욱 이해하기 어렵다. 이는 고전물리학의 논리에 익숙해져 있어서 양자역학의 논리 구조를 따라갈 준비가 안 돼 있기 때문이다. 물에 들어가서 힘을 빼기만 하면 몸이 저절로 뜨는데, 안간힘을 쓰면서 물에 뜨려는 것과 같다.
받아들이기 어려워서 그렇지, 양자역학의 논리는 꽤 간단하다. 측정을 준비하는 단계에서 어떤 측정을 할지를 정하면서 측정값의 범주가 만들어지고, 이 범주가 측정값의 영역을 제한한다. 측정값의 영역이 바뀐 새로운 측정을 하면, 이전 관측의 기억은 어쩔 수 없이 사라지게 된다.
이는 불확정성 원리로도 설명된다. 불확정성 원리에 의하면 두 물리량의 상태를 동시에 규정할 수 없는 경우가 생기는데, 스핀 측정이 양자역학에서 볼 수 있는 가장 좋은 예다. 서로 다른 두 물리량의 상태를 규정할 수 없으므로 두 번째 측정으로 처음의 관측 결과가 사라지고 세 번째 측정으로 두 번째 관측 결과가 사라진다. 이 때문에 위에서 소개한 이상한 일이 벌어진다. 전자는 때로는 과거를 잊기도 한다.
관측으로 대상의 모든 것이 드러나지는 않는다
스핀 측정은 일상생활이나 고전물리학에서의 측정과 상당히 다른 면모를 보여준다. 우리는 무언가를 관측하면 대상 전체를 다 파악했다고 생각한다. 물론 대상의 일부만을 본 것일 테고 그것도 제대로 보지 못한 경우가 대부분이겠지만, 이런 부실한 관측을 하면서 대상을 다 알았다고 착각한다. 북한산을 수백 번 오르더라도 북한산을 안다는 건 불가능한데 말이다.
양자역학은 이런 착각이 원리적으로 불가능하다는 것을 보여준다. 스핀 측정에서는 스핀의 어느 한 방향을 측정하면 다른 방향에 대해서는 전혀 모르게 된다. 이전에 측정했던 정보마저도 사라진다. 우리는 아주 조그만 전자의 스핀마저도 그 전체를 파악하지 못한다. 불확정성 원리가 알려주는 바에 의하면, 그건 기술적으로 불가능한 게 아니다. 원리적으로 불가능하다. 우리는 이 원리적 한계 안에서 세상을 본다. 이게 세간世間이다.
우리가 보는 것은 대상 자체가 아니라, 내가 보는 대상이다
스핀을 측정하면서 우리가 보는 것은 무엇인가? 스핀의 어느 한 성분밖에 볼 수 없지만, 그마저도 그 자체를 보는 게 아니라는 점이 중요하다. 관측에 따라 변하지 않는 그 자체를 볼 수 있다면 처음에 어떤 방향의 스핀을 측정한 다음에 다른 방향의 측정을 한다고 해서 이전에 알아냈던 측정값의 정보가 사라지지는 않을 것이다. 스핀 전체가 아니라 스핀의 어느 한 방향만을 보더라도 관측과 상관없이 변하지 않는 실체란 존재하지 않는다는 것을 양자역학은 보여줬다.(주3)
우리의 일상생활은 양자역학과 아주 다른가? 그렇지 않다. 양자역학과 마찬가지로 우리 몸의 감각이 세상을 보는 데에도 측정값의 범주가 존재한다. 우리 눈은 가시광선 영역의 빛만 볼 수 있고, 우리 귀는 가청주파수 영역의 소리만 들을 수 있다. 모든 감각기관이 다 그렇다. 우리가 보는 것은 대상 자체가 아니라 측정값의 범주 안에서 드러나는 대상의 모습이다. 그래서 돌고래나 고등어에게 바닷물은 짜지 않다.
돌고래에게 바닷물이 짜지 않다는 것은 짠맛이 바닷물의 실체가 아니라는 것이다. 바닷물은 본래 짠 게 아니다. 본래 짜지 않은 바닷물이 나에게 짜게 느껴질 뿐이다. 우리가 보는 것은 세상 자체가 아니다. 그건 내가 보는 세상이고 나에게 나타나는 세상이다. 오온五蘊이 모두 내 마음이 그리는 것이다. 오온五蘊이 연기緣起고 오온五蘊이 공空이다. 이게 세간世間이다. 『화엄경』의 게송으로 글을 맺는다.
心如工畫師 마음은 재주가 많은 화가와 같아서
能畵諸世間 모든 세간을 능히 다 그려낸다.
五蘊實從生 오온이 실로 마음을 따라 일어나는 것이니
無法而不造 이렇게 만들어지지 않은 법이란 없다.
若人知心行 마음이 움직여
普造諸世間 모든 세간을 두루 만들어냈음을 안다면
是人卽見佛 이 사람은 곧 부처님을 본 것이요,
了佛眞實性 부처의 진실한 성품을 깨달아 안 것이다.
<각주>
(주1) (χ축)의 스핀을 측정하기로 결정하면 행렬 s χ 의 고유치 둘 중의 하나가 측정값이 되고 이에 대응하는 고유벡터가 측정 후의 상태가 된다. (y축)의 스핀을 측정하기로 결정하면 행렬 sy 의 고유치 둘 중의 하나가 측정값이 되고 이에 대응하는 고유벡터가 측정 후의 상태가 된다.
(주2) 양자역학이 다루는 모든 물리량에는 1:1로 대응하는 (에르미트)연산자가 존재한다. 어떤 물리량을 측정하려고 한다는 것은 이에 대응하는 연산자를 선택한다는 것이다. 연산자가 선택되면 이 연산자의 고유치가 결정되며, 그 중 하나가 측정값이다. 따라서 물리량을 선택하면, 측정값의 범주가 결정된다.
(주3) 아인슈타인은 어떤 방식의 관측으로도 드러나지 않는 실체가 있어야 한다고 믿었고, 이를 기술하지 못하는 양자역학은 불완전하다고 생각했다. 아인슈타인의 문제 제기 후 55년의 긴 검증 기간을 거친 후, 이런 실체란 존재하지 않는다는 것이 확인됐다. 이에 대한 내용은 개념적으로나 기술적으로 복잡하고 정교한 논의를 포함하고 있어서 이 글에서는 다루지 않는다.
저작권자(©) 월간 고경. 무단전재-재배포금지
|
많이 본 뉴스
-

‘옛거울古鏡’, 본래면목 그대로
유난히 더웠던 여름도 지나가고 불면석佛面石 옆 단풍나무 잎새도 어느새 불그스레 물이 들어가는 계절입니다. 선선해진 바람을 맞으며 포행을 마치고 들어오니 책상 위에 2024년 10월호 『고경』(통권 …
원택스님 /
-

구름은 하늘에 있고 물은 물병 속에 있다네
어렸을 때는 밤에 화장실 가는 것이 무서웠습니다. 그 시절에 화장실은 집 안에서 가장 구석진 곳에 있었거든요. 무덤 옆으로 지나갈 때는 대낮이라도 무서웠습니다. 산속에 있는 무덤 옆으로야 좀체 지나…
서종택 /
-

한마음이 나지 않으면 만법에 허물없다
둘은 하나로 말미암아 있음이니 하나마저도 지키지 말라.二由一有 一亦莫守 흔히들 둘은 버리고 하나를 취하면 되지 않겠느냐고 생각하기 쉽지만, 두 가지 변견은 하나 때문에 나며 둘은 하나를 전…
성철스님 /
-

구루 린뽀체를 따라서 삼예사원으로
공땅라모를 넘어 설역고원雪域高原 강짼으로 현재 네팔과 티베트 땅을 가르는 고개 중에 ‘공땅라모(Gongtang Lamo, 孔唐拉姆)’라는 아주 높은 고개가 있다. ‘공땅’은 지명이니 ‘공땅…
김규현 /
-

법등을 활용하여 자등을 밝힌다
1. 『대승기신론』의 네 가지 믿음 [질문]스님, 제가 얼마 전 어느 스님의 법문을 녹취한 글을 읽다가 궁금한 점이 생겨 이렇게 여쭙니다. 그 스님께서 법문하신 내용 중에 일심一心, 이문二…
일행스님 /
※ 로그인 하시면 추천과 댓글에 참여하실 수 있습니다.
댓글목록
등록된 댓글이 없습니다.